Zerstören Depotschwankungen dein Vermögen? (Volatility Drag Myth Busting)

Sie waren schrecklich.

Ich habe sie geliebt.

Die Rede ist von den grauen Männern aus Michael Endes ‚Momo‘, der Standardliteratur meiner Jugend für große Kinderaugen.

Nun, es scheint, dass sich die grauen Männer seit ihrem bitteren Ende weiterentwickelt haben. Sie sind moderner geworden. Sie sind jetzt im Finanzbereich unterwegs. Dort klauen sie auch keine Zeit mehr – hat heutzutage eh keiner mehr. Sie klauen jetzt Rendite.

Graue Anzüge und Zigarren sieht man auch nicht mehr. Ihre einzige Spur: Schwankungen von Anlageprodukten. Hältst du Anlagen in deinem Depot, die viel hoch- und runtergehen? Dann kannst du sicher sein: Du hast graue Männer im Depot.

An die Geschichte von Momo erinnert mich jedenfalls, was man in vielen Internetforen und selbst bei respektierten Finanzbloggern liest (die nennen es nur anders, weil sie nichts von den grauen Männern wissen):

Wenn man Anlagen mit hoher Volatilität hält – also Anlagen, deren Wert viel hin und her schwankt –, müsse man sich im Klaren sein, dass die tatsächlich über die Jahre verdiente Rendite dadurch negativ beeinflusst wird. Durch den Effekt hätte man am Ende schlicht weniger übrig, als es gemäß der durchschnittlichen jährlichen Verzinsung der Anlage eigentlich sein müsste. Dieser Unterschied werde umso größer, je höher die Volatilität ist.

Volatilität vernichte also Rendite und damit eigentlich verdientes Vermögen gleich mit; je stärker die Schwankungen, umso mehr Rendite verschwinde im Nichts.

Was ist dran an diesem mit Volatility Drag bezeichneten Phänomen? Klauen starke Schwankungen tatsächlich die Butter vom Renditebrot? Zieht Volatilität die Rendite nach unten?

In diesem Artikel betreiben wir ordentlich Myth Busting: Wir zeigen, warum der Schluss falsch ist, erklären, was wirklich hinter dem Phänomen steckt, und warum es besser Volatility Lift statt Volatility Drag heißen sollte.

Los geht es auf einen Deep Dive durch die dunklen und unendlichen Weiten der Renditeweltraumes.

Was ist der Volatility Drag?

Der Volatility Drag ist einer der besten Brain Twister der Finanzmarkttheorie.

Und mein liebster.

Viele Quellen im Internet warnen vor ihm. Ein Beispiel ist etwa dieser Artikel vom Finanzwesir (den bewundere ich für seine ständig sprudelnden Wort- und Geschichts-Assoziationen – für dieses Bekenntnis kann er schon mal als Beispiel herhalten).

Zur Veranschaulichung nehmen wir allerdings nicht sein kompliziertes 5-Perioden-Beispiel, sondern etwas Einfacheres (ist aber zumindest ebenfalls von ihm).

Die Geschichte geht so:

Es gibt eine hochvolatile Anlage (die linke). Wenn ich 1.000 EUR dort investiere, habe ich am Ende des zweiten Jahres 700 EUR übrig. Nicht so toll. Wir haben 300 EUR verloren.

Jetzt reduzieren wir die Volatilität: wir halbieren die Schwankungen einfach mal und – nein, wir legen noch einen drauf und nehmen von der positiven Rendite im zweiten Jahr sogar noch fünf Prozentpunkte weg (rechnen also mit +15 % statt +20 %). Sonst bleibt alles gleich. Insbesondere ist der Durchschnittswert der beiden Anlagen gleich. Er bleibt bei exakt -5 %.

Und nun? Am Ende des zweiten Jahres bleiben plötzlich 862,50 EUR übrig, ganze 162,50 EUR mehr.

Ist das nicht unglaublich? Diese präzise, stille, kalt-mechanische Eleganz, mit der die grauen Männer zugeschlagen haben? Volatilität vernichtet Vermögen. Quod erat demonstrandum.

Ich gebe freimütig zu, auch ich habe den Volatility Drag in früheren Jahren nicht ganz richtig verstanden. Man muss seine Hirnwindungen schon ein paar Runden um das Phänomen herumwickeln, bevor die Verbindung hält. Es ist ja auch so verdammt intuitiv und naheliegend: Wir verwenden ‚Volatilität‘, um das Risiko einer Anlage zu messen. Risiko hat so etwas Negatives an sich, das will niemand in seinem Depot haben. Im Kopf ist es von dort nur ein klitzekleiner Sprung hin zu der Stelle, an der man der Volatilität auch noch zutraut, dass sie einem die Rendite vom Brot klaut.

Nicht leichter wird die Sache dadurch, dass Verzinsung über mehrere Perioden exponentiell wirkt. Da wird es nicht-linear und ziemlich anstrengend. Nichts für unseren Kopf. Einfach so aufsummieren funktioniert da nicht mehr.

Das sieht man wunderbar, wenn man mal überlegt, wie viel Rendite es nach einem einmal erlittenen Verlust braucht, um wieder zurück zur Nulllinie zu kommen

Nach 10 % Miese im ersten Jahr brauche ich nur eine ein wenig höhere Rendite von gut 11 % zurück zur Wasseroberfläche. Ist das Minus jedoch erst einmal bei -50 % angekommen, müssen es von da unten schon ganze 100 % Rendite sein, um den Einbruch ungeschehen zu machen. Je größer der Verlust, umso überproportional mehr braucht es für den Weg zurück.

Willkommen in der wundersamen Welt der Mehrperioden-Zinsrechnung.

Was ist für uns Investoren wirklich relevant?

Bevor wir weitermachen, gehen wir erst einmal ein Stück in uns und überlegen: Was ist eigentlich das Wertvolle an einem Investment für uns aus finanzieller Sicht? Nach welchem Kriterium sollen wir Investitionen vergleichen?

Ich würde sagen: Nach dem was hinten rauskommt. Die beiden Beispiele da oben haben denselben Mittelwert. Durchschnitte können wir aber nicht essen. Wir können uns nur von dem etwas kaufen, was am Ende im Depot ist.

Wie rechnet man das aus?

Nehmen wir tausend Euro und investieren ihn in die linke Zeitreihe. Dann haben wir nach einem Jahr:

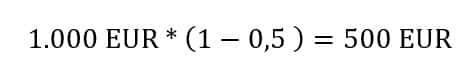
oder für beide Jahre auf einmal:

Wichtig hier für gleich: Die Zinssätze der einzelnen Jahre müssen wir miteinander multiplizieren – nicht addieren.

Was an der Argumentation nicht stimmt

Das Beispiel ganz oben geht davon aus, dass die beiden Zeitreihen ‚bis auf die Volatilität gleich‘ sind, weil sie denselben durchschnittlichen Zinssatz (dasselbe arithmetische Mittel) aufweisen.

Zwei Erklärungen, warum die beiden Beispiele oben nicht ‚gleich‘ sind, und das arithmetische Mittel als Kriterium für uns nichts taugt:

1) Die intuitive
Wir haben im rechten Beispiel gesagt, dass wir ‚mal alle Zinszahlen halbieren‘. Halbieren ist eine lineare Änderung: Egal wie hoch jede Zahl, ich nehme einfach die Hälfte davon. Verzinsen funktioniert aber eben nicht linear (siehe obiges Beispiel zum Ausgleich eines Verlustes). Wenn ich von 100 Kastanien 50 wegnehme und dann 50 wieder dazulege, habe ich wieder 100. Mit Renditen geht das nicht. Stumpfes Halbieren ignoriert den Zinseszins-Effekt. Ist die linke Zeitreihe ein Apfel, macht das Halbieren daraus eine Birne, die wir nicht mehr mit dem Apfel vergleichen können.

2) Die mathematisch einleuchtende
Das arithmetische Mittel ist eine lineare Summe aus den Renditen (eine ganz einfache ‚Linearkombination‘): Wir zählen darin alle Renditen zusammen. Wir haben aber gerade gesehen, dass sich unser Vermögen am Ende durch Multiplizieren berechnet, nicht durch Zusammenzählen (wir haben die Klammern oben miteinander mal genommen). Zinsen über mehrere Perioden sind eben nicht-linear – und lassen sich deshalb auch nicht durch eine lineare Summe wie das arithmetische Mittel ausdrücken.

Zum Vergleich von Investitionen ist das arithmetische Mittel also ungefähr so geeignet wie ein Schraubenzieher zum tieferen Verständnis von Quantenmechanik.

Entsprechend sind die beiden Beispiele oben durch das Halbieren eben alles andere als ‚gleich‘. Sie haben nichts miteinander zu tun. Sie haben nur zufällig (oder hinkonstruiert) denselben einfachen Mittelwert – der für uns nichts aussagt.

Den Geometern sei dank

Können wir so einen Durchschnitt gar nicht ausdrücken?

Glücklicherweise haben sich schon die Alten Griechen über ähnliche Dinge den Kopf zerbrochen. Es gibt tatsächlich eine Zahl, die die durchschnittliche Verzinsung einer Anlage korrekt anzeigt: die geometrische Rendite.

Die erhalten wir, wenn wir die Berechnung oben ein wenig umformen.

Aus

wird dann die geometrische Rendite

Die ist für eine Investorin der einzig wahre Durchschnitt. Die Zahl, an der wir uns festhalten können.

Das sehen auch viele Menschen in englischsprachigen Ländern so. Und so findet man diesen Wert in Prospekten, Reportings und auf Websites ganz oft als CAGR (Compound Annual Growth Rate, durchschnittliche jährliche Wachstumsrate).

Was ist jetzt mit dem Volatility Drag?

Um das alles zusammenzubringen, machen wir ein neues Experiment. Ähnlich wie ganz oben. Diesmal achten wir aber darauf, dass die jährlichen Zinsen so gestrickt sind, dass sie die Anfangssumme nach zwei Jahren immer exakt verdoppeln.

Es gibt unendlich viele mögliche Kombinationen. Ein paar Beispiele:

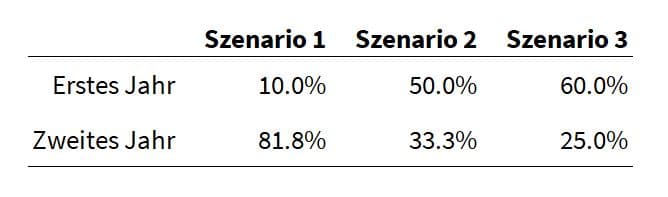
Gibt es im ersten Jahr beispielsweise 10 %, muss ich im zweiten Jahr 81,82 % verdienen, um mein Geld zu verdoppeln. Bringt das erste Jahr 50 %, brauche ich wegen des Zinseszinseffekts im zweiten Jahr nicht 50 %, sondern nur gute 33 % für die Verdoppelung usw.

In einen Graphen gepackt sieht das dann so aus: Unterschiedliche Zinssätze des ersten Jahres sind nach rechts angetragen, die Zinssätze, die im zweiten Jahr davon abhängig jeweils zur Verdoppelung führen, nach oben.

Kurzes Nachrechnen: in jedem Fall liegt die Durchschnittsverzinsung (geometrische Rendite oder CAGR) genau bei 41,42 %. Für eine Investorin sind alle diese Kombinationen gleichwertig: Jede verdoppelt mein Geld nach zwei Jahren. Der Rest kann mir erst einmal wurscht sein.

Jetzt wird’s spannend: Was passiert, wenn wir für jedes einzelne dieser Geld verdoppelnden Renditepaare das arithmetische Mittel berechnen? Sieht so aus (auf der Achse nach rechts sind die Zinspaare angetragen, sortiert nach dem Satz des ersten Jahres).

An dem Punkt, an dem beide Renditen identisch sind (Zins im Jahr 1 = Zins im Jahr 2 = 41,42 %) stimmen geometrisches und arithmetisches Mittel exakt überein. Dort ist die Volatilität über beide Jahre null. Aber an den Rändern, da wo die Renditepaare unterschiedlicher werden – man kann auch sagen ‚wo die Volatilität höher wird‘ – geht das arithmetische Mittel langsam immer weiter in die Höhe.

Und was ist daran jetzt so besonders?

Na, nichts eben. Das ist der Volatility Drag.

In einem Satz zusammengefasst: Je unterschiedlicher die Renditen über die Jahre sind, umso stärker weicht das arithmetische Mittel vom geometrischen Mittel ab.

Das ist alles. Der Volatility Drag ist nichts weiter als ein einfacher mathematischer Zusammenhang ohne größere Bedeutung für uns Investoren. Weder vermindert hohe Volatilität Rendite, noch bekomme ich mehr Rendite dadurch, dass ich Schwankungen vermeide.

Sieht man für Investoren gleichwertige Zeitreihen an – also diejenigen mit dem gleichen Vermögen am Ende und der gleichen geometrischen Durchschnittsrendite – ist das Einzige, was bei höherer Volatilität passiert, das Aufblähen des arithmetischen Mittels. Es wäre also viel treffender, wenn wir das Phänomen ‚Volatility Lift‘ oder vielleicht noch besser ‚Volatility Inflation‘ nennen würden, statt ‚Volatility Drag‘.

Menschen mögens einfach

Warum hält sich der Mythos ‚Volatilität klaut Rendite‘ so hartnäckig?

Ich kann mir das nur so erklären: Das menschliche Gehirn ist nicht für Denken über exponentielles Wachstum gemacht. So ein einfaches arithmetische Mittel ist uns schon von Haus aus viel sympathischer. Also tendieren wir dazu, uns mit ihm zu identifizieren, uns also quasi auf diesen Mittelwert ‚drauf zu stellen‘ und die Welt von dort aus zu betrachten. Und nun sehen wir doch glatt mit dem Fernglas am Horizont eine sinkende geometrische Rendite bei steigender Volatilität. Weil wir nicht auf unsere Füße achten, merken wir aber gar nicht, dass wir wegen der aufgeblähten arithmetischen Rendite zwar immer noch ‚gleich hoch‘ stehen, aber in Wirklichkeit jetzt auf dem Rücken eines ganz anderen, schlechteren Anlagevehikels.

Man kann auch sagen, der Schluss ist tautologisch (das Lieblingswort meines früheren Chefs): Wir vergleichen ein gutes und ein schlechteres Investment miteinander und kommen zu dem Schluss, dass das schlechtere schlechter ist.

Was ist nun die Moral von der Geschicht?

• Volatilität frisst sich nicht in dein Vermögen. Weder Volatilität noch graue Männer klauen dir etwas von deiner Rendite.
• Um eine durchschnittliche Rendite über die Zeit zu berechnen, darfst du NIEMALS (NIEMALS bedeutet wirklich NIEMALS) das einfache arithmetische Mittel verwenden. Diese Zahl sagt über mehrere Perioden nichts aus.
• Um eine durchschnittliche Rendite verschiedener Anlagen in derselben Zeitperiode auszurechnen (z. B. von allen deinen ETFs im letzten Jahr) ist das arithmetische Mittel dagegen bestens geeignet – weil dort nichts hintereinander verzinst wird, also das Ergebnis einer Periode nicht danach in einer anderen weiterverzinst wird.
• Volatilität per se ist nicht unbedingt schlecht. Das Hinzufügen einer sehr volatilen Anlage zu deinem Portfolio kann deine Rendite sogar steigern.
• Für uns ist die Volatilität des Gesamtportfolios entscheidend, nicht die Volatilität einzelner Anlagen darinnen.
• Statt einzelne Bausteine nach geringer Volatilität auszuwählen, solltest du lieber auf der Ebene deines Gesamtportfolios denken und nach möglichst unkorrelierten (aber vielleicht volatilen) Bausteinen suchen und sie entsprechend gewichten.
• Es ist für uns tatsächlich besser, ein möglichst gleichförmig steigendes Portfolio mit niedriger Volatilität zu halten. Aber das hat nichts mit verschwundener Rendite zu tun, sondern mit dem Sequence-of-Returns-Risiko. Und weil es psychologisch leichter ist, in so ein Portfolio investiert zu bleiben.

Eine völlig unwichtige Nebenbemerkung zum Schluss

Kennst du den Goldenen Schnitt? Ein sehr krummes Verhältnis von zwei Längen zueinander, das in der Natur ständig vorkommt und wir z. B. auf Fotos als besonders ästhetisch wahrnehmen. Mich verblüfft immer wieder, wie scheinbar völlig unterschiedliche Dinge bei näherer Betrachtung zusammenhängen. Dieser Goldene Schnitt ist nichts anderes als das geometrische Mittel der beiden Längen.

Wenn dir dieser Myth Buster gefallen hat, abonniere unseren Newsletter. Dann versäumst du keinen neuen Artikel mehr.